
3.1 소개
전파 전파(이하 Radio propagation)
- 번역이 조금 어색함
무선 이동 통신 채널은 하나의 무선 단말과 다른 하나의 무선 단말 사이에 시간적으로 변화하는 통신 경로로 모형화 한 것이다.
- 첫 번째 단말: 기지국에 있는 고정안테나
- 두 번째 단말: 이동국이나 이동 중인 가입자
위의 상황은 빠른 페이딩(Fast fading)을 유발하는 Multi path Radio propagation 유발한다.
이동 무선 전파
- 전 방향성 안테나
- 반송파 주파수의 선정
- Fast fading 환경에서의 전송 방식의 선택
- 등등 새로운 도전(?)이 필요
Multi path channel 환경에서의 radio propagation
- 안테나의 높이
- 빌딩들의 배치
- 나무, 도로, 주변 지형 등에 좌우 됨
해당 Chapter에서는 적절한 통계적 기법을 이용하여 Mobile Radio Propagation 환경을 설명 하고자 한다.
3.2 무선 파동의 유형
| 구분 명칭 | 약어 | 주파수 대역 | 특징 |
|---|---|---|---|
| 초저주파 | ELF (Extremely Low Frequency) | < 300 Hz | 지상파 |
| 음성대역 | ILF (Infra Low Frequency) | 300 Hz ~ 3 kHz | 지상파 |
| 초장파 | VLF (Very Low Frequency) | 3 kHz ~ 30 kHz | 지상파 |
| 장파 | LF (Low Frequency) | 30 kHz ~ 300 kHz | 지상파 |
| 중파 | MF (Medium Frequency) | 300 kHz ~ 3 MHz | 지상파/공중파 |
| 단파 | HF (High Frequency) | 3 MHz ~ 30 MHz | 공중파 |
| 초단파 | VHF (Very High Frequency) | 30 MHz ~ 300 MHz | 우주파 |
| 극초단파 | UHF (Ultra High Frequency) | 300 MHz ~ 3 GHz | 우주파 |
| 센티미터파 | SHF (Super High Frequency) | 3 GHz ~ 30 GHz | 우주파 |
| 밀리미터파 | EHF (Extra High Frequency) | 30 GHz ~ 300 GHz | 우주파 |
| 극고주파 | THF (Tremendously High Frequency) | 300 GHz ~ 3000 GHz | 우주파 |
3.3 Radio propagation의 원리
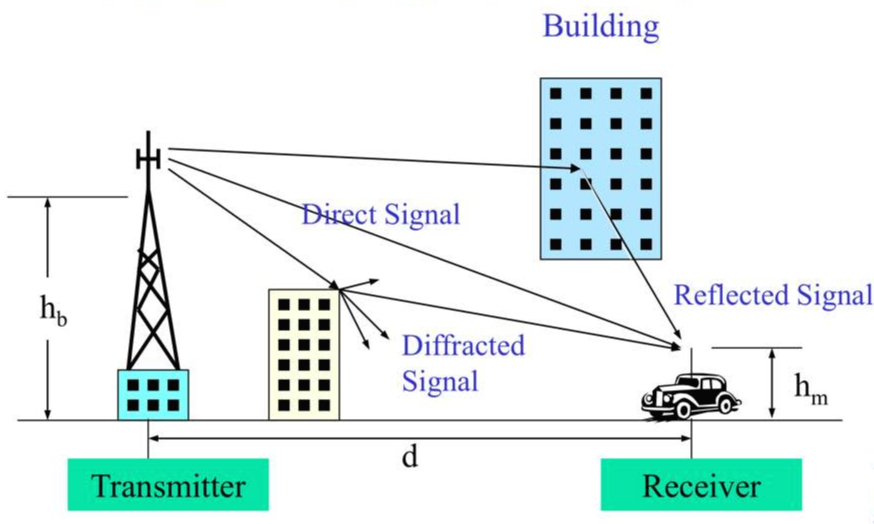
- 반사: Propagation되는 파동이 그 파동의 파장보다 큰 장애물에 부딪힐 경우 반사 됨
- 지구의 표면 큰 빌딩, 큰 벽면 등
- 회절: 송신국과 수신기 간의 무선 경로가 날카롭고 불규칙적인 모서리를 만날 때 발생하는 현상
- 직접 경로가 없는 상황에서도 파동은 장애물을 돌아서 굽어짐
- 산란: 장애물이 파동의 파장보다 작은 경우에는 입사되는 파동이 여러 갈래의 미약한 신호들로 반사되는 현상
- 나뭇잎이나 도로 표지판, 가로등 등등
Multipath의 결과
3.4 자유 공간에서의 Radio propagation
- 자유 공간
- 공기라는 매질이 있는 공간
- 장애물이 없는 상황
- 전력 신호 $P_t[W]$를 전송하는 등방향성 점원에서 방사된 전력은 이 점원으로부터 임의의 거리, d만큼 떨어진 지점에서 보면 일정 반경을 가진 구의 표면에 균등하게 분포 됨
- 해당 식을 아래와 같이 표현할 수 있음
$$
P_r=\frac{A_e\cdot G_t\cdot P_t}{4\pi d^2}
$$- Ae: 전송 안테나의 유효 면정
- Gt: 전송 안테나의 이득
- 수신 안테나의 유효 개구면과 이득 사이의 관계는 다음과 같이 얻어 짐
$$
G_r=\frac{4\pi A_e}{\lambda^2}
$$ - Gr을 Pr식에 대입
$$
P_r=\frac{G_rG_tP_t}{\left(\frac{4\pi d}{\lambda}\right)^2}
$$ - 자유공간 손실 Lf는 다음과 같음
$$
L_f=\frac{P_t}{P_r}\
= \frac{1}{G_rG_t}\cdot \left(\frac{4\pi d}{\lambda}\right)^2
$$ - 여기서 자유공간은 Gt = Gr = 1인 상황으로 아래와 같이 표현 됨
$$
L_f = \left(\frac{4\pi d}{\lambda}\right)^2 = \left(\frac{4\pi f_cd}{c}\right)^2
$$ - 자유공간 손실을 dB로 표현하면 아래와 같음
$$
L_f(dB) = 32.45 + 20\cdot log_{10}{f_c(MHz)} + 20\cdot log_{10}{d(km)}
$$
3.5 지상 Radio propagation
- 지상 mobile wireless 채널은 기지국과 단말기 간의 통신으로 특징지어짐
- 이 채널은 fading현상이 있는 multipath radio propagation 환경을 이룸
- 신호는 전파 경로상에 존재하는 여러 가지 장애물들로 인한 회절과 반사로 인하여, 많은 서로 다른 경로를 통하여 목적지에 다다르게 된다는 의미
- 수신 신호의 전력 Pt는 다음과 같이 표현
$$
P_r = \frac{G_tG_rP_t}{L}
$$ - 위 식에서 L은 채널에서의 radio propagation 손실을 나타냄
- Radio는 세 가지 요소에 의하여 특정지어짐
- Path loss
- Slow fading
- Fast fading
L = L_PL_SL_F\
L_P:\mbox{Path loss}\
L_S:\mbox{Slow fading}\
L_F:\mbox{Fast fading}
$$
3.6 Path loss (경로 손실)
- 지상 radio propagation에서의 경로 손실은 다음과 같음
$$
L_P = Ad^\alpha
$$- A 및 α: radio propagation 상수
- 통상, α는 대표적인 도심에서 3~4정도의 값을 가짐
- d: 기지국과 단말기 사이의 거리
- A 및 α: radio propagation 상수
1. 도시환경
$$
L_{PU}(dB)=69.55+26.16log_{10}{f_c(MHz)}-13.82log_{10}{h_b(m)}-\alpha[h_m(m)]+[44.9-6.55log_{10}{h_b(m)}]\cdot log_{10}{d(km)}\\
\mbox{식}
\begin{cases}
L_{PU}(dB)=&-10log_{10}{L_{PU}}\\
f_c,&\mbox{반송파 주파수 (150~1500 HMz)}\\
h_d,&\mbox{기지국의 유효 안테나 높이 (1~10 m)}\\
d,&\mbox{거리 (1m ~ 20km)}\\
\alpha(h_m),&\mbox{단말기의 안테나 높이를 조정하는 인자}
\end{cases}
$$
- α(hm)은 상황에 따라 다름
- a. 큰 도시
$$
\alpha[h_m(m)]=[1.1log_{10}{f_c(MHz)-0.7}]h_m(m)-[1.56log_{10}{f_c(MHz)}-0.8]
$$
b. 중소 도시
$$
\alpha[h_m(m)]=
\begin{cases}
8.29[log_{10}{1.54h_m(m)}]^2-1.1, &f_\psi < \mbox{300 MHz}\\
3.2[log_{10}{11.75h_m(m)}]^2-4.97, &f_\psi > \mbox{300 MHz}
\end{cases}
$$
2. 도시 근교
$$
L_{PS}(dB)=L_{PU}(dB)-2\left[log_{10}\cdot\frac{f_c(MHz)}{28}\right]^2-5.4
$$
3. 환히 트인 지역
$$
L_{PO}(dB)=L_{PU}(dB)-4.78[log_{10}{f_c(MHz)}]^2-18.33log_{10{f_c(MHz)}}-40.94
$$
3.7 Slow fading
- Slow fading 환경에서는 거리가 d인 지역에서의 지역 평균값 rm(d)는 다음과 같이 정의
$$
r_m(d)=\frac{1}{2d_w}\int^{d+d_w}_{d-d_w}r(x){dx}
$$ - 이 식에서 r(x)는 위치 x에서의 수신 신호이며, dW는 윈도우의 크기를 의미
- r(x)는 slow fading과 fast fadint의 곱으로 표현이 가능
$$
r(x)=r_s(x)r_f(x)
$$ - 새롭게 표현된 r(x)를 rm의 식에 대입하면 다음의 관계를 얻을 수 있음
$$
r_m(d)=\frac{1}{2d_w}\int^{d+d_w}_{d-d_w}{r_s(x)r_f(x)}{dx}
$$ - 이 식에서 x = d일 경우, rs(d)는 해당 지역의 실제 수신 신호의 평균 세기인 것으로 정함
$$
r_m(d)=r_s(d)
$$ - 따라서 통계적 수치에 근거하여 윈도우의 크기 dw는 다음의 조건을 만족해야 함
$$
\frac{1}{2d_w}\int^{d+d_w}_{d-d_w}{r_f(x)}{dx} \rightarrow 1
$$ - 위의 r_s=r_f는 단말의 위치에 대한 함수임을 알 수 있음
- 거리는 속도와시간의 함수이므로(즉, x=v_t), r_s=r_f는 다음과 같이 표현
$$
r(t)=r_s(t)r_f(t)
$$ - Slow fading은 대부분 대수 정규분포를 가짐
- 이 경우, 수신 신호 크기의 확률 밀도 함수는 dB단위로 표현할 때는 아래와 같음
$$
p(M)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(M- \bar{M})}{2\sigma^2}}
$$ - M은 실제 수신 신호의 크기 m을 dB 단위로 표현한 것
- \sigma는 dB 단위의 표준편차를 의미
$$
p(m)=\frac{1}{\sqrt{\pi m}\sigma_0}e^{-\frac{log_10{\frac{m}{\bar{m}}}}{2\sigma_0^2}}
$$
3.8 Fast fading
'DAN lab. > DAN lab. Master's 1 Summer' 카테고리의 다른 글
| 04-02. Channel Coding and Error Control (0) | 2021.07.15 |
|---|---|
| 04-01. Channel Coding and Error Control (0) | 2021.07.14 |
| 02-03. 확률, 통계 및 트래픽 이론 (0) | 2021.07.07 |
| 02-02. 확률, 통계 및 트래픽 이론 (0) | 2021.07.07 |
| 02-01. 확률, 통계 및 트래픽 이론 (0) | 2021.07.07 |